Just Do IT !

Python算法学习day2:查找和排序(一)

Python算法
字数统计: 838阅读时长: 3 min
2020/01/16 Share

说明

排序算法是《数据结构与算法》中最基本的算法之一。

排序算法可以分为内部排序和外部排序

内部排序是数据记录在内存中进行排序。

而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

用一张图概括：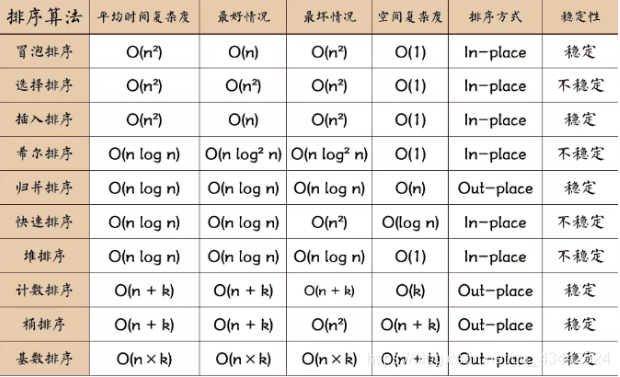
在这里插入图片描述

关于时间复杂度：

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。
线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；
O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序
线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。
关于稳定性：
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

1. 查找

(1) 列表查找

1
2
3
4
5
def linear_search(data, value):
	for i in range(len(data)):
		if data[i] == value:
			return i
	return 0

此算法时间复杂度为O(n)

(2) 二分查找

1
2
3
4
5
6
7
8
9
10
11
def bin_search(data, value):
	low = 0
	high= len(data) - 1
	while low <= high:
		mid = (low + high) // 2
		if data[mid] == value:
			return mid
		elif data[mid] > value:
			high = mid - 1
		else data[mid] < value:
			low = mid + 1

时间复杂度为O(logn)

(3) LeetCode704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。


示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1


提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        low = 0
        high = len(nums)-1
        while low <= high:
            mid = (low + high) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                low = mid + 1
            else:
                high = mid - 1
        return -1

2. 排序

(1) 冒泡排序

1
2
3
4
5
def bubble_soft(li):
	for i in range(len(li) - 1):
		for j in range(len(li) - i - 1):
			if li[j] > li[j+1]:
				li[j], li[j+1] = li[j+1], li[j]

  • 时间复杂度：O(n²)

  • 空间复杂度：O(1)

  • 健壮性：健壮

  • 难易程度：简单

优化:如果列表已经排序完成,则可提前中断排序

1
2
3
4
5
6
7
8
9
def bubble_soft(li):
	for i in range(len(li) - 1):
		exchange = False
		for j in range(len(li) - i - 1):
			if li[j] > li[j+1]:
				li[j], li[j+1] = li[j+1], li[j] 
				exchange = True
		if not exchange:
			break

(2) 选择排序

1
2
3
4
5
6
7
def select_soft(li):
	for i in range(len(li)-1):
		min_pos = i
		for j in range(i+1, len(li)):
			if li[min_pos] > li[j]:
				min_pos = j
		li[i], li[min_pos] = li[min_pos], li[i]

(3) 插入排序

1
2
3
4
5
6
7
8
def insert_sort(li):
	for i in range(1,len(li)):
		tmp = li[i]
		j = i - 1
		while j >= 0 and li[j] > tmp:
			li[j+1] = li[j]
			j-=1
		li[j+1] = tmp

以上就是一些简单的查找和排序经典算法,再接再厉,每日学习一点算法,然后温故而知新

原文作者：浩翰

原文链接：https://plutoacharon.github.io/2020/01/16/Python算法学习day2-查找和排序-一/

发表日期：January 16th 2020, 8:47:31 pm

更新日期：February 3rd 2020, 6:11:51 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 说明
    1. 1.1. 关于时间复杂度：
  2. 2. 1. 查找
    1. 2.1. (1) 列表查找
    2. 2.2. (2) 二分查找
    3. 2.3. (3) LeetCode704. 二分查找
  3. 3. 2. 排序
    1. 3.1. (1) 冒泡排序
    2. 3.2. (2) 选择排序
    3. 3.3. (3) 插入排序
Total : 190
2020
2019
CTF Liunx 高可用负载均衡 Java Hadoop Docker Esxi Dokcer Flume GitHub Kafka Golang Golang日志收集系统 Hbase Hive Git Kali Kubernetes Shell Python算法 Spark Sqoop Vmware 机器学习 Zookeeper PHP Hexo 安全 Python PySpark Maven 网络 数据采集 CDN AWD ZooKeeper
CTF Liunx Hadoop Docker GitHub Golang Golang日志收集系统 高可用负载均衡 Hive Java Kubernetes 其他 Python算法 Spark Vmware 机器学习 博客 Python 网络 CDN