Just Do IT !

Python算法学习day6:堆排序(二叉树)

Python算法
字数统计: 586阅读时长: 2 min
2020/01/19 Share

堆

在学习堆排序之前,先必须了解一下什么是堆

堆是具有以下性质的完全二叉树：

每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。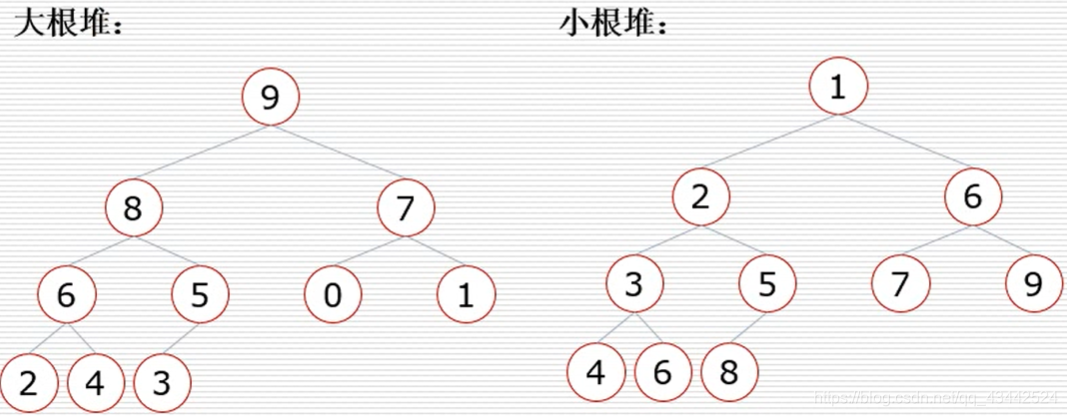
在这里插入图片描述
而二叉树中,父节点与左右孩子节点的编号下标都有一定的关系:
其中父节点与左孩子节点的关系是 i -> 2i+1, 父节点与右孩子节点的关系是 i -> 2i+2

注: 这里指节点的下标关系

堆的向下调整性质

假设: 节点的左右字数都是堆,但自身不是堆

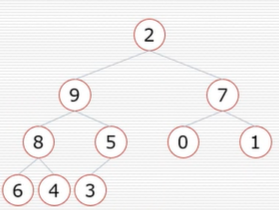
在这里插入图片描述
当根节点的左右字数都是堆时,可以通过一次向下的调整来将其变换成一个堆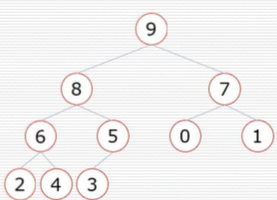
在这里插入图片描述

挨个出数

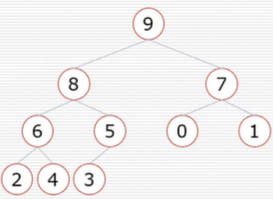
在这里插入图片描述
9是堆中数字最大,将9取出,为保证完全二叉树,将树中最后的数字3添加到头部.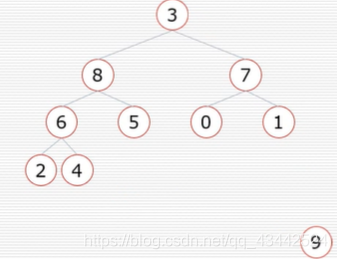
在这里插入图片描述
接下来向下调整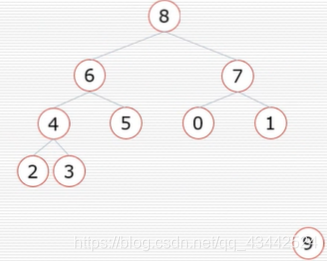
在这里插入图片描述
依次取数便取出一个升序列表

堆排序的平均时间复杂度为 Ο(nlogn)

堆的算法步骤

  1. 创建一个堆 H[0……n-1]；

  2. 把堆首（最大值）和堆尾互换；

  3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；

  4. 重复步骤 2，直到堆的尺寸为 1。

来源：https://github.com/hustcc/JS-Sorting-Algorithm

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def sift(li, low, high):
	# li表示数, low表示树根, high表示树最后一个节点的位置
	tmp = li[low]
	i = low
	j = 2 * i + 1 # 指向左孩子
	# i指向空位, j表示两个孩子
	while j <= high: # 循环退出的第二种情况: j > high, 说明空位i是叶子节点
		if j+1 <= high and li[j] < li[j+1]: # 如果右孩子存在并且比左孩子大, 指向右孩子
			j += 1
		if li[j] > tmp:
			li[i] = li[j]
			i = j
			j = 2 * i + 1
		else: # 循环退出的第一种情况, j位置的值比tmp小, 说明两个孩子都比tmp小
			break
	li[i] = tmp

def heap_sort(li):
	n = len(li)
	# 1. 构造堆
	for low in range(n//2-1, -1, -1):
		sift(li, low ,n-1)
	# 2. 挨个出数
	for high in range(n-1, -1, -1):
		li[0], li[high] = li[high], li[0]
		sift(li, 0, high - 1)

原文作者：浩翰

原文链接：https://plutoacharon.github.io/2020/01/19/Python算法学习day6-堆排序-二叉树/

发表日期：January 19th 2020, 5:37:35 pm

更新日期：January 19th 2020, 5:37:54 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 堆
    1. 1.1. 堆的向下调整性质
    2. 1.2. 挨个出数
  2. 2. 堆的算法步骤
  3. 3. 算法实现
Total : 190
2020
2019
CTF Liunx 高可用负载均衡 Java Hadoop Docker Esxi Dokcer Flume GitHub Kafka Golang Golang日志收集系统 Hbase Hive Git Kali Kubernetes Shell Python算法 Spark Sqoop Vmware 机器学习 Zookeeper PHP Hexo 安全 Python PySpark Maven 网络 数据采集 CDN AWD ZooKeeper
CTF Liunx Hadoop Docker GitHub Golang Golang日志收集系统 高可用负载均衡 Hive Java Kubernetes 其他 Python算法 Spark Vmware 机器学习 博客 Python 网络 CDN