全排列
LeetCode 46. 全排列
1 | 给定一个没有重复数字的序列,返回其所有可能的全排列。 |
方法1:使用库函数itertools.permutations
Python 中文文档3.7.2rc1itertools
1 | # 方法一 |
方法二:回溯1
2
3
4
5
6
7
8
9
10nums = [1,2,3]
res = []
def backtrack(nums, tmp):
if not nums:
res.append(tmp)
return
for i in range(len(nums)):
backtrack(nums[:i] + nums[i+1:], tmp + [nums[i]])
backtrack(nums, [])
print(res)
回溯算法框架:
解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
代码方面,回溯算法的框架:1
2
3
4
5
6
7
8
9
10result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」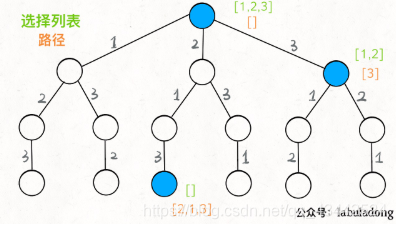
二进制枚举
定义
先给出子集的定义:子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。
用途
在写程序的时候,有时候我们可能需要暴力枚举出所有的情况,这时可以考虑通过二进制来枚举子集来尝试解决问题。
解释
假设我们现在有5个小球,上面分别标号了0,1,2,3,4代表这些小球的权值,现在要像你求出这些小球的权值可以组成的所有情况。
假设我们现在有5个小球,上面分别标号了0,1,2,3,4代表这些小球的权值,现在要像你求出这些小球的权值可以组成的所有情况。
我们用二进制的思维来考虑这个问题,因为有5个小球,所以我们用5个比特位来分别标记小球存在还是不存在,对于这样一种情况,比如我们现在要选择3个小球,分别是0,3,4号小球,那么我们用二进制1表是当前的小球存在,用0表示当前小球不存在
| 二进制下标 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 二进制 | 1 | 1 | 0 | 0 | 1 |
小球状态| 存在| 存在| 不存在 |不存在| 存在|
我们可以用5个比特位来表示这种情况,如果小球全部选择的话那么二进制表示就是11111,二进制的11111转化为十进制数字就是31,这个数字正好就是2^5 -1,那么我们可以用从0~(2^5−1)这些数表示完所有的选取状态(因为这个范围内的二进制数情况正好包括了这些选取状况).
所以我们遍历每一个集合:
for i in range(1<<n):
设s = 1(二进制为00001)代表我们选0位置上的数值;
那么我们如何找到每个位置上的数值呢?
我们遍历的是二进制的十进制表示,我们当然可以转化为二进制再枚举每一位,但是,这很麻烦;
一个很巧妙的方式就是利用位运算。
1<<0=1(0);
1<<1=2(10);
1<<2=4(100);
1<<3=8(1000);
1<<4=16(10000);
...
1<<7=128(10000000);
...
看出来了吧!我们只需要将n&(1<<i)我们便可以得到每一位是不是1 (1<< i 除了那一位,剩余的都是0,所以我们就可以得到那一位是不是1)
按位与运算符(&)
参加运算的两个数据,按二进制位进行“与”运算。
运算规则:0&0=0; 0&1=0; 1&0=0; 1&1=1;
即:两位同时为“1”,结果才为“1”,否则为0
例如:3&5 即 0000 0011& 0000 0101 = 00000001 因此,3&5的值得1。
左移运算(<<)
a << b就表示把a转为二进制后左移b位(在后面添b个0)。例如100的二进制为1100100,而110010000转成十进制是400,那么100 << 2 = 400。
可以看出,a << b的值实际上就是a乘以2的b次方,因为在二进制数后添一个0就相当于该数乘以2(这样做要求保证高位的1不被移出)。
题目举例:
忧郁的JM,借酒消愁。略微喝醉的他,和下酒花生聊起了天。
JM:“你知道质数是什么吗?”
花生:“……”
JM:“质数是指在大于11的自然数中,除了11和它本身以外不再有其他因数的自然数。”
花生:“……”
JM:“现在我有一个质数集合{3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 53, 59, 61, 67, 71, 97, 101, 127, 197, 211, 431}3,5,7,11,13,19,23,29,31,37,41,53,59,61,67,71,97,101,127,197,211,431,你可以从中挑出任意多个(0-12个)不同的数出来构成一个新数(取出数的和)”
JM:“构成的新数从小到大依次为:0, 3, 5, 7, 8, 10, 11, 12, 13…,0,3,5,7,8,10,11,12,13…,你知道[0, 1694][0,1694]中有多少个数是没法构成的吗?”
花生:”……“
JM:“例如:1,2,4…1,2,4…均是不能够从质数集合中挑数构成”
你来帮帮花生吧~
思路:
总共 22 个数,选择其中的 0 -12 个数,加上来组成一个新数。
我们可以用二进制枚举,对于 22 个数,每一个数,只有拿或不拿两种情况,也就是 0 或者 1。所以总共有 2 ^ 22 约等于 4e6。不会超时。
因为我们用二进制枚举,每一位对应这个数要不要取,如果取,那就累和。还要注意,最后只能取 12 个,所以我们要判断,这种取法中 1 的个数,如果是 >12 ,那这种方案不成立。
然后算出所有情况的数,用 set 统计(可能有重复的,去重)。
最后答案是问,无法构成的个数,因此答案是 : 总数(1695) - set 中的数(可以构成了这么多数)
1 | nums = [3,5,7,11,13,19,23,29,31,37,41,53,59,61,67,71,97,101,127,197,211,431] |